■ 주성분 분석 (PCA, Principal Component Analysis)
- 주성분 분이란 변수가 가지고 있는 정보의 손실을 최소화 하면서 변수의 차원을 축소하는 분석 기법이다.
■ 차원 축소의 필요성
- 설명 변수(feature)가 많으면 학습 속도가 느려진다.
- 의미 없는 feature들로 인해서 과적합이 되거나 학습이 제대로 되지 않는다.
- 차원을 축소하면 데이터를 시각화로 표현하기 쉽다.
■ 차원의 저주

■ 주성분 분석의 필요성
- 데이터의 feature가 늘어날 때마다 차원은 증가한다.
- 차원이 증가할수록 공간의 부피가 기하급수적으로 증가하면서 데이터의 밀도가 매우 낮아진다.
- 1차원에서는 데이터의 밀도가 3/10으로 전체 데이터의 약 30%를 포함
- 2차우너에서는 데이터의 밀도가 1/10으로 전체 데이터의 약 10%를 포함
- 3차원에서는 데이터의 밀도가 0/10으로 해당 공간에서는 포함된 데이터가 없음
- 즉, 차원이 과도하게 높아지면 각 객체들 사이의 거리가 늘어나게 되고(sparse), 그만큼 저차원일 때보다 더 불안정하기 때문에 과적합 문제로 이어질 수 있다.
■ 주성분 분석의 활용처는?
- 훈련 알고리즘의 속도를 높이기 위해 (PCA가 적용된 데이터 세트를 이용하여 지도학습 수행)
- 고차원 데이터를 3차원 이하로 축소하여 시각화하고 데이터의 특성을 파악하기 위해
- 이미지 데이터의 노이즈 제거를 위해
■ PCA의 원리
- 가장 높은 분산을 가지는 데이터의 축을 찾아 이 축으로 차원을 축소한다.
- 분산은 데이터 정보를 설명하는 중요한 통계량이다.
- 주성분은 데이터들의 분산이 가장 큰 방향을 뜻하는 벡터다.
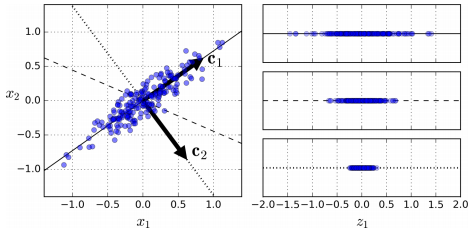
- 오른쪽 그림은 좌측 (x1, x2) 벡터를 특정 벡터에 내적(기하학적으로는 정사영)하여 투영한 결과이다.
- 실선(C1)의 투영은 최대 분산을 유지하고, 점선(C2)는 매우 작은 분산만 유지하고 있다.
- 따라서, 가장 큰 분산을 유지하는 축을 선택하는 것이 정보 손실이 적기 때문에 C1축이 첫 번째 주성분이 된다.
- 그렇다면 데이터를 어떤 벡터에 내적하는 것이 최적의 결과라고 할 수 있을까?
- 이 문제를 해결하기 위해 사용할 수 있는 것이 공분산 행렬이다.
■ 공분산 행렬
- 하나의 특성 값 사이에서의 변동을 분산이라고 하며, 두 개 이상의 특성 값 사이에서의 변동을 공분산이라고 한다.
- 데이터의 구조를 설명해주며, 특히 특성들 간의 변동이 얼마나 닮았는가를 나타내는 행렬이다.
- 예를 들어 x와 y 특성 변수가 있을 때 x가 커질 때 y도 함께 커지거나, x가 작아질 때 y도 같이 작아지면 두 값을 곱했을 때 양수가 된다. 반면에 x가 커질 때 y는 작아지거나, x가 작아질 때 y가 커지면 두 값을 곱했을 때 음수가 된다.
- 이와 같이 숫자의 크기와 부호를 이용해서 관계의 방향과 경향을 알려주는 것이 공분산이다.
※ 육상선수 종목별 기록표

- 표 자체로는 데이터의 구조나 경향을 찾기 힘들다. 즉, 어떤 종목을 잘하면 다른 종목도 잘하는 경향이 있는지, 만약 그렇다면 어떤 종목들이 서로 이러한 경향성에 있어서 상대적으로 밀접한 것인지를 알기 힘들다.
- Player-1 선수의 경우 허들 종목에서의 편차는 +0.58이고 높이뛰기 종목에서의 편차는 +0.05이며, 이 두 편차의 곱은 0.029이다. 즉, 두 편차의 곱이 양인 경우 한 종목에서 평균보다 뛰어나면서 동시에 다른 한 종목에서도 평균보다 뛰어나다는 점을 의미한다. 만약 두 편차의 곱이 음인 경우에는 어떤 종목에서 평균보다 잘하면 다른 한 종목에서는 평균보다 못하는 경향이 있다는 뜻이다.
※ 두 종목에 대하여 모든 선수들에게 이와 같은 두 편차들의 곱을 구한 후 이를 평균하는 수식은 다음과 같다.

※ 위 수식이 바로 공분산이며 x의 편차와 y의 편차를 곱한 것의 평균을 의미한다.

- 선수들의 종목별 기록들을 보여주는 데이터를 가지고 구한 공분산행렬
- 공분산행렬은 정방행렬이며 대칭행렬이다.
- 대각 성분에는 자기 자신의 분산이며 나머지 성분은 서로 다른 두 변수간의 공분산 값이다.

■ 주성분 분석 (PCA)
- 차원 축소를 위한 방법인 변수 추출에는 기존 변수 중 일부만 활용하는 방식이 있고, 모두 쓰는 방식이 있는데 PCA는 후자에 해당한다. 이러한 PCA는 기존 변수를 선형결합(Linear Combination)해서 새로운 변수를 만들어 낸다.
- PCA는 변수가 d개, 관측치가 n개 있는 데이터 X(n x d)로 새로운 변수 z를 아래와 같은 과정을 통해 만들어진다.
- 입력 데이터의 공분산 행렬을 구한다,
- 공분산 행렬을 고유값 분해 해서 고유 벡터와 고유값을 구한다,
- 고유값이 가장 큰 k개의 고유 벡터를 추출
- 고유값이 가장 큰 순으로 추출된 고유벡터를 이용해 입력 데이터들을 선형 변환 (내적)
■ 공분산 행렬의 고유값 분해 의미
- 고유 벡터와 교유 값 정의 : 벡터가 회전하지 않고 확대나 축소만 할 때, 변화된 벡터의 길이 비율이 고유값이 되고 그때의 벡터 방향이 고유벡터가 된다.
- 따라서 고유 벡터는 그 행렬이 벡터에 작용하는 주축(principal axis)의 빙향을 나타내므로 공분산 행렬의 고유 벡터는 데이터가 어떤 방향으로 분산되어 있는지를 나타내 준다고 할 수 있다.
- 고유값은 고유 벡터 방향으로 얼마만큼의 크기로 벡터공간이 늘려지는지를 얘기한다. 따라서 고유값이 큰 순서대로 고유 벡터를 정렬하면 결과적으로 중요한 순서대로 주성분을 구하는 것이 된다.


'데이터 분석 > 머신러닝' 카테고리의 다른 글
| [ML] 13. 고유값 분해를 통한 PCA (0) | 2023.11.27 |
|---|---|
| [ML] 12. PCA 공분산 이해하기 (0) | 2023.11.24 |
| [ML] 11. K-Means Clustering (0) | 2023.11.24 |
| [ML] 비지도학습 알고리즘 - 군집분석 (0) | 2023.11.23 |
| [ML] 데이터 분석 실습 (비행기 연착 추측 분류) (0) | 2023.11.23 |